Describe How Bernoulli's Principle and Equation Is Used With Technology

The Bernoullis equation is one of the most useful equations that is applied in a wide variety of fluid flow related problems. This equation can be derived in different ways eg.

Bernoulli S Equation

The cleaning sequence itself is automatic and continuous.

. Bernoullis equation can be understood though manipulation of the energy of a flowing fluid. Explore within the context of the Bernoulli. More complex flow behavior can be explained with modified versions of Bernoullis principle.

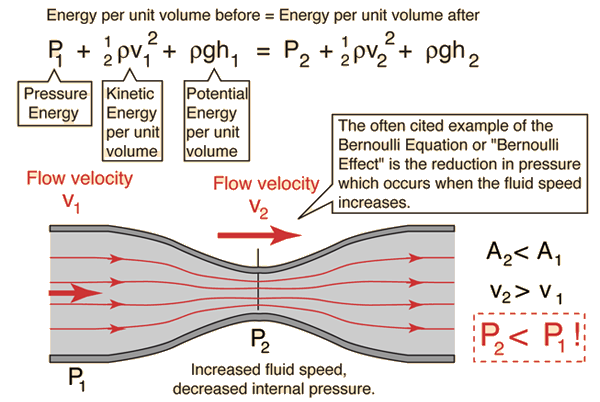
According to the Venturi effect as fluid velocity increases the pressure decreases and vice versa. Where 𝜃 is the angle between the normal of the streamline and the vertical z-axis at that point m 𝜌V 𝜌 dA ds is the mass W mg 𝜌g dA ds is the weight of the fluid particle and sin 𝜃 dzds. The Venturi effect describes how the rate of fluid flow in an enclosed system changes as the flow enters a constricted channel.

Bernoullis principle and its corresponding equation are important tools in fluid dynamics. 24 indicates that the downstream flow depth must be smaller than the upstream one ie. According to Bernoullis principle faster moving air exerts less pressure and therefore the air must exert an upward force on the airfoil as a result of a pressure difference.

Relate the Bernoulli Principle to the lift one of the. The speed of a fluid air in this case determines the amount of pressure that a fluid can exert. Bernoullis principle is used to calibrate the airspeed indicator so that it displays the indicated airspeed appropriate to the dynamic pressure.

Four forces of flight. We know that the work done on the fluid was due to conservation of gravitational force and change in kinetic energy. However there are a few important assumptions that are made during the derivation of this formula which makes this powerful equation not necessarily the most useful in many biofluid mechanics applications although as.

P 1 1 2ρv12ρgh1 P 2 1 2ρv22ρgh2 P 1 1 2 ρ v 1 2 ρ g h 1 P 2 1 2 ρ v 2 2 ρ g h 2. Let the subscripts 1 and 2 refer to any two points along the path that the bit of fluid follows. The Bernoullis equation can be considered to be a statement of the conservation of energy principle appropriate for flowing fluids.

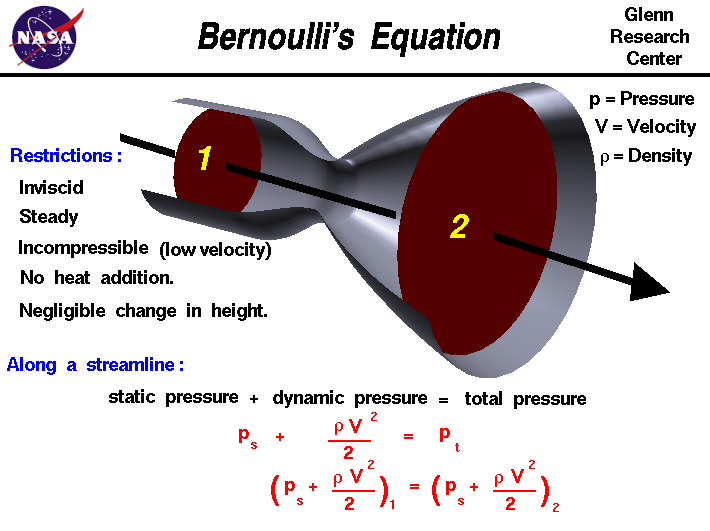
D 2 d 1 provided that E 2 15 d c. P 1 p 2 gz v 2 2 is constant along any stream line where p 1 is the fluid pressure p 2 is the mass density of the fluid v is the fluid velocity g is the acceleration due to gravity and z is the vertical height above a. It can be applied to various types of fluid flow resulting in various forms of Bernoullis equation.

Determine that though two items look identical they may not have the same density. P dA P dP dA W sin 𝜃 mV dVds. Bernoullis principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure.

An aeroplane wing works by splitting the air and sending part of the air over the top curved surface and part below the wing along the flat surface. The Bernoulli equation helps us deduce the waters speed that will flow into the plant turbines of a hydroelectric plant. Bernoullis principle is a universal relation describing flow behavior for ideal fluids.

DW p 1 dV p 2 dV p 1 p 2 dV. Bernoulli equation An equation that describes the conservation of energy in the steady flow of an ideal frictionless incompressible fluid. The shape of an airfoil causes air to flow faster on top than on bottom.

The distinguishing feature of a Bernoulli Filter is a disc mounted on a pneumatic cylinder which enables contactless cleaning of the filter. The principle states that there is reduced pressure in areas of increased fluid velocity and the formula sets the sum of the pressure kinetic energy and. It puts into a relation pressure and velocity in an inviscid incompressible flow.

This change in fluid flow rate through a channel can be described using Bernoullis principle. Hence the downstream specific energy is the smallest. Bernoullis Equation and Principle.

This means that a fluid with slow speed will exert. The change in kinetic energy of the fluid is given as. Bernoulli System pioneered the application of the Bernoulli Principle named after the Swiss scientist Daniel Bernoulli to water filtration.

The Venturi effect and Bernoullis equation makes statements about conservation of energy conservation of momentum and conservation of mass. Bernoullis equation has a wide application of uses from wing design to pipe flow. 38 A De Laval nozzle utilizes Bernoullis principle to create a force by turning pressure energy generated by.

Lift coefficient as a function of Angle of Attack. Bernoullis principle can be derived from the principle of conservation of energy. The Bernoulli equation is a useful formula that relates the hydrostatic pressure the fluid height and the speed of a fluid element.

For B 1 B 2 the graphical solution Fig. Bernoullis principle also known as Bernoullis equation will apply for fluids in an ideal state. By integrating Eulers equation along a streamline by applying first and second laws of thermodynamics to steady irrotational inviscid and in-compressible flows etc.

It might be conceptually simplest to think of Bernoullis principle as the fact that a fluid flowing from a high pressure region to a low pressure region will accelerate due to the net force along the direction of motion. This is known as the Bernoulli principle. The attachment of pipe for water flow to the town is connected at a lower height.

Bernoulli principle states that the upstream and downstream total heads must be equal. Bernoullis equation is a. The idea that regions where the fluid is moving fast will have lower pressure can seem strange.

D K 1 2 m 2 v 2 2 1 2 m 1 v 1 2 1 2 ρ d V v 2 2 v 1 2 The change in potential energy is given as. Some relations from fluid dynamics are universal and one of these is. This is the core example that helps us to understand the application of this principle effectively.

Some common applications of Bernoullis principle are its use to explain flow behavior in simple systems. Explore the Bernoulli Principle which states that. Therefore pressure and density are inversely proportional to each other.

Hence the downstream specific energy is the smallest. Bernoullis equation is a mathematical representation of this. It is one of the most importantuseful equations in fluid mechanics.

The Dutch-Swiss mathematician Daniel Bernoulli discovered that where there is an increase in the velocity of fluid there is a decrease in the pressure.

Verification Of Bernoulli S Equation Using Venturimeter Fluid Practicals

Bernoulli Equation

What Are The Limitations Of The Bernoulli Principle Quora